Back to Opengl

It’s been over a year since I’ve written GLSL shader code, and well over two years since I worked on a project that required shader programming on a daily basis. This is largely because my focus has been on ray tracing and physically based rendering techniques. I’m starting to get back into developing with OpenGL as it makes more sense for what I’m working on now.

Switching to GL from nearly a year of software based ray tracing is certainly a unique feeling. It’s somewhat like jumping into a chilled swimming pool — after the initial shock passes things are pretty much okay. On the CPU there are very few limitations in terms of data access, especially with ray tracing since real time execution isn’t a central goal. Shader programming is on the other end of the spectrum, both in terms of render throughput and programming style.

GLSL

One thing I did notice though is that all of my preconceived notions of how shaders and geometry should be used for are now gone. While it is true that vertex data is intended for displaying surfaces and fragment programs are designed to shade those surfaces, the potential use cases are much more flexible. This week I’ve been working on a shader-based vector graphic renderer that can draw shapes like rounded rectangles and circles, as well simple Bezier Curves. In general the input geometry itself only defines the outer frame for the shape and has little bearing on the final result. The vertex shader stage is used to determine where the shape should be drawn. For example, with Bezier Curves the input triangles define the control points for the curve and the fragment shader draws the curve. The following curve was renderer with a single triangle:

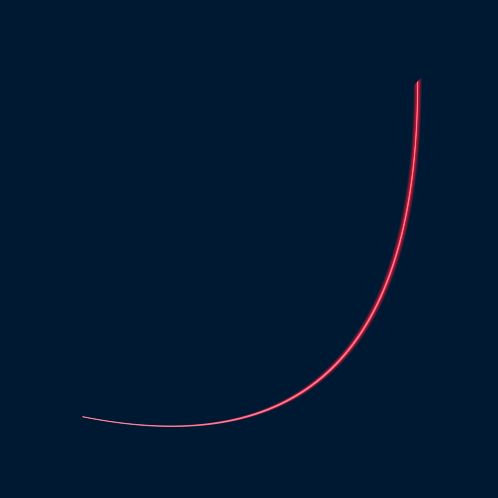
The end result is a smooth curve that maintains a crisp edge at any zoom level since it is independent of the geometry resolution. Additional effects can easily be added — in the previous image the white line is the curve itself, while the pink region is controlled by a variable stroke width. Modifying the position of the control points changes the shape of the curve:

I’m not entirely sure what the end goal of the curve rendering is. The original idea was to create a sort of calligraphy rendering tool that uses mouse velocity to determine stroke width. So far I’ve just enjoyed messing with shaders again, so I’ll probably continue experimenting rather than working on a specific project.

GPU Architecture

The other area I’ve been reading up on is modern GPU architecture and how shader programs are actually executed. The subtle details are quite interesting, and certain aspects of OpenGL/Direct3D make a lot more sense when put into the right context. For example the mechanisms that controls fragment program execution are particularly neat and also have some noteworthy performance implications.

A fragment program is a piece of shader code that executes for each sample in the raster process. These are sometimes referred to as pixel shaders, particularly in Direct3D land, however there isn’t always a one-to-one mapping between fragments and screen pixels. Inputs to a fragment shader that originate in an earlier stage in the pipeline are typically interpolated based on the fragment’s position.

Of course GPUs don’t execute things serially – fragment shading is a highly parallelizable task and modern hardware exploits this quite well. One of the neat implementation details is that fragments are actually processed in blocks of 2x2. Each block is run on a thread group and the fragment instructions are execute in lock-step, so at a given time all four fragments are performing the same instruction.

Performance benefits aside, this has one particularly cool implication that I only recently discovered. For any expression or variable in a fragment shader, it’s possible to get partial derivatives with respect to x and y in fragment coordinate space. In GLSL this is done with the dFdx()and dFdy() built-in functions, and with ddx() and ddy() in HLSL. The derivatives are approximated using finite differences within the 2x2 fragment block. For example, given some block of GLSL:

vec3 test = vec3(in_texcoord, time*0.2);
test += in_position;
vec3 partial_x = dFdx(test);

The value of partial_x will be the the rate of change of the test variable in the X direction, evaluated at the current fragment position. Since all four fragments in the block are always performing the same operations, they’re all guaranteed to have computed their value of test at the same time. This means that when a particular fragment starts executing the dFdx() function, it can safely look up the value of test in each of its neighbours and use that to approximate the derivative.

The only caveat is that the derivative functions produce undefined behavior when invoked as part of a non uniform branch. For example, consider the following GLSL snippet:

vec3 test = vec3(in_texcoord, time*0.2);
test += in_position;

if (test.x > 0.5)
{
    vec2 broken = vec2(test.yz);
    vec2 partial_x = dFdx(broken);
}

There’s no guarantee that all four fragments will enter the if statement, therefore some may not compute a value for broken. Executing dFdx in the conditional will fetch values from the registers that would have held broken in each of the neighbours, but since the computation was never performed garbage data will be retrieved. This is why it’s generally incorrect to use a texture sampler inside non uniform control flow, as indicated by the GLSL manual. If there’s a guarantee that all invocations of the shader program will take the same branch then using dFdx is perfectly fine.

The blocked nature of fragment processing also has performance implications, again in the case of non uniform branching. Since all the processing must remaining in lockstep, if one fragment needs to enter a branch while the other three don’t, the non-branching fragments must stall execution until the branch is completed. A given block can only be executing a single instruction at a time, so no additional work can be done while waiting.

This is particularly bad for performance in the case of an else statement:

if ([non-uniform-condition])
    [big computation]
else
    [other big computation]

When [big computation] is executing, fragments that failed the conditional test will wait as described above. Once that computation is complete, those fragments will stall and wait for the other set of fragments to complete the else block. Assuming that both sides of the branch are taken frequently, the run time of the above statements will be fairly close to time(big computation) + time(other big computation) for each fragment — in effect, the fragment will perform as if it takes both branches all of the time.